
1.
int main ()
{
int i ;
int j = k + 1 ; // unknown variable k: type checker
int a[] = {1,2,3} // missing semicolon: parser
j = a + 6 ; // addition of integer to array: type checker
a[4] = 7 ; // too big array index: runtime
printf("hello world\n) ; // unterminated string: lexer
// no return of type int: type checker
}
2.
0001 0000 1111 1111 bipush -1
0001 0000 0010 0000 bipush 32
0110 0100 isub
0001 0000 0000 1001 bipush 9
0110 1000 imul
(-1 - 32) * 9
3.
while (x > y) y = x = 3 ;
AST:
SWhile (EGt (EIdent (Ident "x")) (EIdent (Ident "y")))
(SExp (EAss (Ident "y") (SExp (EAss (Ident "x") (EInt 3)))))
4. Numerals
N0, NP. Num ::= "0" | Pos
PD, PPD, PP0. Pos ::= Dig | Pos Dig | Pos "0"
D1,... Dig ::= "1" | "2" | "3" | "4" | "5" | "6" |"7" | "8" | "9"
NP (PPD (PP0 (PP0 (PD D2))) D7)
5. Unix
Script ::= [Line] ; Line ::= [Command] In Out ; In ::= "<" Ident | ; Out ::= ">" Ident | ; Command ::= Ident [Opt] [Arg] ; Arg ::= File ; Opt ::= "-" Ident ; [Opt] ::= Opt [Opt] | ; [Arg] ::= Arg [Arg] | ; [Command] ::= Command "|" [Command] | Command ;
6. Lisp
entrypoints Program;
Prog. Program ::= [Def] ;
terminator Def "";
Defun. Def ::= "(" "defun" LIdent "(" [LIdent] ")" Expr ")" ;
separator LIdent "" ;
EApp. Expr ::= "(" [Expr] ")" ;
EAtom. Expr ::= LIdent ;
EQuote. Expr ::= "'" Expr ;
separator Expr "" ;
token LIdent letter (letter | '.')* ;
comment ";" ;
7. Regular expressions
entrypoints RegExp ; EUnion. RegExp ::= RegExp "|" RegExp1; ESeq. RegExp1 ::= RegExp1 RegExp2 ; EKleene. RegExp2 ::= RegExp3 "*" ; EChar. RegExp3 ::= Char; EIdent. RegExp3 ::= Ident ; coercions RegExp 3 ;
8. Comments
'/' '*' (char - '*' | '*' (char - '/'))* '*'* '*' '/'
9. DFA for comments

10. Stripping tags in Alex:
%wrapper "basic"
tokens :-
\< [^>]* \> ;
([.\n] # \<)+ { \s -> s }
{
main = do s <- getContents
putStr (concat (alexScanTokens s))
}
11. Tracing LR parsing
| Stack | Input | Action | |
|---|---|---|---|
| while (x > 4) {x = x-1; } | |||
| while | (x > 4) {x = x-1; } | shift | |
| while ( | x > 4) {x = x-1; } | shift | |
| while ( x | > 4) {x = x-1; } | shift | |
| while ( Exp2 | > 4) {x = x-1; } | reduce | |
| while ( Exp1 | > 4) {x = x-1; } | reduce | |
| while ( Exp | > 4) {x = x-1; } | reduce | |
| while ( Exp > | 4 ) {x = x-1; } | shift | |
| while ( Exp > 4 | ) {x = x-1; } | shift | |
| while ( Exp > Exp2 | ) {x = x-1; } | reduce | |
| while ( Exp > Exp1 | ) {x = x-1; } | reduce | |
| while ( Exp > Exp | ) {x = x-1; } | reduce | |
| while ( Exp | ) {x = x-1; } | reduce | |
| while ( Exp ) { | x = x-1; } | shift | |
| while ( Exp ) { x | = x-1; } | shift | |
| while ( Exp ) { x = | x-1; } | shift | |
| while ( Exp ) { x = x | -1; } | shift | |
| while ( Exp ) { x = Exp2 | -1; } | reduce | |
| while ( Exp ) { x = Exp1 | -1; } | reduce | |
| while ( Exp ) { x = Exp1 - | 1; } | shift | |
| while ( Exp ) { x = Exp1 - 1 | ; } | shift | |
| while ( Exp ) { x = Exp1 - Exp2 | ; } | reduce | |
| while ( Exp ) { x = Exp1 | ; } | reduce | |
| while ( Exp ) { x = Exp | ; } | reduce | |
| while ( Exp ) { Exp | ; } | reduce | |
| while ( Exp ) { Exp ; | } | shift | |
| while ( Exp ) { Stm | } | reduce | |
| while ( Exp ) { Stm [Stm] | } | reduce | |
| while ( Exp ) { [Stm] | } | reduce | |
| while ( Exp ) { [Stm] } | shift | ||
| while ( Exp ) Stm | reduce | ||
| Stm | reduce | ||
Doing this by cheating (the smart way):
Compile with BNFC:
bnfc -m Ex.cf
make
Regenerate the parser as a debugging one
happy -dag ParEx.y
Recompile the parser
ghc --make TestEx.hs -o TestEx
Parse the statement
echo "if (x + y > 4) if (true) {x = y = y - 1 ;} else 8 ;" | ./TestEx
What you see begins
state: 0, token: 9, action: shift, enter state 20 state: 20, token: 1, action: shift, enter state 23 state: 23, token: 13, action: shift, enter state 14 state: 14, token: 3, action: reduce (rule 6), goto state 9 state: 9, token: 3, action: reduce (rule 12), goto state 10
12. Left-recursive grammar
S ::= S "x" S ::=
| Stack | Input | Action | |
|---|---|---|---|
| S | x x x x | reduce | |
| S x | x x x | shift | |
| S | x x x | reduce | |
| S x | x x | shift | |
| S | x x | reduce | |
| S x | x | shift | |
| S | x | reduce | |
| S x | shift | ||
| S | reduce | ||
Right-recursive grammar
S ::= "x" S S ::=
| Stack | Input | Action | |
|---|---|---|---|
| x | x x x | shift | |
| x x | x x | shift | |
| x x x | x | shift | |
| x x x x | shift | ||
| x x x x S | reduce | ||
| x x x S | reduce | ||
| x x S | reduce | ||
| x S | reduce | ||
| S | reduce | ||
13. Generate a Happy file with BNFC, and change the code that builds abstract syntax trees into
Exp1 :: { Double }
Exp1 : Exp1 '+' Exp2 { $1 + $3 }
| Exp1 '-' Exp2 { $1 - $3 }
| Exp2 { $1 }
Exp2 :: { Double }
Exp2 : Exp2 '*' Exp3 { $1 * $3 }
| Exp2 '/' Exp3 { $1 / $3 }
| Exp3 { $1 }
Exp3 :: { Double }
Exp3 : Double { $1 }
| Integer { fromIntegral $1 }
| '(' Exp ')' { $2 }
Exp :: { Double }
Exp : Exp1 { $1 }
Makefile:
eval:
alex LexArith.x
happy EvalArith.y
ghc --make -o eval EvalArith.hs
14. Copy.cf
Ids. S ::= [Ident] ; terminator Ident "" ;
diff_ParCopy_y
28c28
< S : ListIdent { Ids (reverse $1) }
---
> S : ListIdent { let xs = reverse $1 in if copies xs then Ids xs else error "not a copy" }
38a39,41
> copies :: [Ident] -> Bool
> copies xs = let (xs1,xs2) = splitAt (div (length xs) 2) xs in xs1 == xs2
>
15. Count.hs
module Count where
import AbsCode
import ComposOp
import Data.Map
import ErrM
count :: Stm -> String
count = unlines . Prelude.map show . assocs . flip transStm empty
type Result = Map Ident Int -> Map Ident Int
transIdent :: Ident -> Result
transIdent x = case x of
_ -> insertWith (const (+1)) x 1
transStm :: Stm -> Result
transStm x = case x of
SWhile exp stm -> transExp exp . transStm stm
SBlock stms -> \m -> foldr transStm m stms
SExp exp -> transExp exp
transExp :: Exp -> Result
transExp x = case x of
ESub exp0 exp -> transExp exp0 . transExp exp
EGt exp0 exp -> transExp exp0 . transExp exp
EAss x exp -> transIdent x . transExp exp
EId x -> transIdent x
_ -> id
16. Derivation of validity
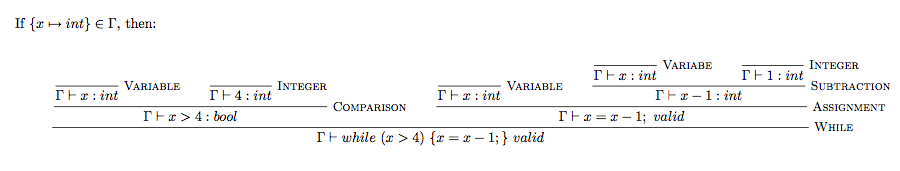
17. Typing rules

20. If statements with else.
Counterexample:if (x++ == 0) stm1 else stm2
Better translation:
if (exp) stm1 else stm2 ==> {
bool b = exp;
if (b) stm1
if (!b) stm2
}
where b is a variable name that is not used in exp,
stm1 or stm2.
Another, very elegant translation (added by AR after class in 2010, suggested by a participant):
if (exp) stm1 else stm2 ==> if (exp !! (stm1,false)) stm2
which uses the "comma expression" of C: first execute stm1, then return false.
This works because disjunction is lazy.